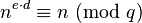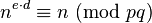有朝一日,量子電腦真的能成為事實,除了速度快以外,它還能做到許多當前電腦做不
到的事。目前,量子電腦已經由「史前時代」進入了「實驗時代」了,人們在找尋更多
適用於量子電腦的計算法則,以能充分發揮量子電腦的功效。雖然,我們還不知道量子
電腦的研究何時才會變成工程問題,但是,目前的成就已足使每個人振奮了。
讀過費因曼 (R. P. Feynman) 的故事的人都知道, 他也曾應聘於某電腦公司去設計電
腦。物理學家,怎麼也設計起電腦來了?原來,當電腦越作越小,速度越來越快,量子
力學的效應就不能不考慮了。五十年來、幾乎每隔兩年,電腦的速度就加快了一倍。大
家可以想想,身邊的個人電腦。 從十幾年前的蘋果二號電腦,到現在的 586 就是一個
例子。但是,這個趨勢會繼續下去嗎?總有一天,路會走到盡頭。無論如何快,訊號傳
遞的速度不會快於光速。無論積體電路做得如何小,總不會小過原子。當這一天來臨時
, 怎麼辦?這個世界將變成什樣子?其實,幾十年前 IBM 公司的 R. Landauer 及 C.
H. Bennett 就已經在考慮這個問題了。 他們要問的問題是;到底電路元件,最小可以
做到多小?計算過程中,最少要花多少能量?電腦,無論如何也該遵守物理定律。例如
,熱力學就告訴我們:一個引擎的效率有一定的極限。那麼,對於量子電腦,是否也有
某些物理極限存在呢?
80 年代初期, P. Benioff 告訴我們, 原則上量子電腦是可行的。 後來有英國的 D.
Deutsch 及美國、以色列等的其它一些人,也做過一些研究。不過 80 年代中期,這股
熱潮卻又衰退了。主要原因是:他們研究的量子電腦,「非常的抽象」;討論的問題總
是,例如, 貝爾不等式、多世詮釋 (many-worlds interpretation)、EPR 悖論‧‧‧
等等。而且跡象顯示,量子電腦很容易出錯,確不容易修正。不過費因曼卻認為,量子
電腦,仍有研究的價值,可能可以用來模擬其它的量子系統。但是,它能以更高的速度
解其它的數學問嗎?
過去三年來,情況有所改觀 1993 年 S. Lloyd 找到了一堆可以作為量子電腦的系統。
P. W. Shor 更告訴我們:量子電腦可以做因數分解; 一個傳統電腦中重要卻又困難的
問題。而且它計算所需的時間,只與該數的對數成多項式關係;這是傳統電腦所作不到
的。 這個結果令人振奮。 大家討論的重點已經實際到, 例如, H. F. Chau 及 F.
Wilczek 討論如何設計邏輯元件 [1] 及 B. Schumacher 討論量子編碼及資料壓縮、傳
輸之類的了。[2]
量子資訊
資訊,本來就是離散的東西了。但是這與「量子資訊」還是不太一樣。在一般的電腦裡
,我們用電位的高低代表「零」與「壹」,進而組成各種資訊。在量子電腦裡,我們用
原子的能階來代表資訊的「零」與「壹」。 用氫原子的基態表示「零」 ( 記為 | 0 >
),激發態表示「壹」 ( 記為 | 1 > )。一個位元的量子資訊,稱為 qubit,可以是這
兩個狀態的線性組合; 代表該位元在某一瞬間的狀態。 這種狀態, 我們稱為聚相態
(coherent states)。 如此一串氫原子就可以組成各種資訊了。但是,要組成一個電腦
,要能處理這些資訊,還需要一些邏輯元件來進行運算;要能讀入運算單元,進行處理
,再輸出儲存。因此,一個量子電腦必須要能讀、寫及運算。 1944 年諾貝爾物理獎得
主,I. I. Rabi,最早告訴我們如何將資訊寫入量子系統。以氫原子為例吧!假設,這
個氫原子原本是處於基態, 能量為 E0,要寫入一個位元為「零」的資訊不必做任何處
理。要寫入一個位元為「壹」的資訊,則可用適當頻率之雷射將原子激發至 E1 的能階
。如果原子本來就在激發態,這個雷射就會使它放出光子,變成基態。
其實電子並不是說跳就跳上去的。它還是「慢慢」的跳上去的。這點,用物質的波動性
質來看就清楚了。電子,就像是個在盪鞦韆的小孩。外面的雷射光,就像在推這個小孩
的大人。如果他推的頻率正確,小孩就會越盪越高。直到這個電子的能量等於這兩個能
階的能量差,E1 - E0,電子就跳上去了。 因為,電子所在的狀態,可以用基態的波函
數及激發態的波函數的線性組合來表示,當電子能量越來越高,激發態所對應的振幅也
就越來越大。如果這個雷射光只作用了一半的時間,電子就在一個由基態及激發態各半
所組成的狀態。這就是量子電腦與傳統電腦不同的地方:任何時候 | 0 > 與 | 1 > 同
時存在,只是比例不盡相同而已。也正因為這點,量子電腦可以做到傳統電腦做不到的
事。
讀與寫是一樣的原理:但是所使用的雷射光頻率是足以使 E1 能階的電子跳躍到一個更
高,卻不穩定,的能態 E2。 如果原子本來在 E1 能階,電子會跳到 E2 能階,但隨即
又跳回 E1 能階,且放出光子。如果原子本來在 E0 能階,由於能量不合電子則不會轉
移。如果是在上述的「中間狀態」,則它被讀為「零」與讀為「壹」的機率各半。
量子運算
電子元件一般可分為線性,例如電阻及電容,及非線性,如二極體及電晶體,兩種。線
性元件直接改變輸入的訊號,非線性元件卻會使多個訊號交互作用。例如擴大機之所以
能調整聲音的音調,高低音,完全是由非線性元件,電晶體,所造成。音調的改變,是
由輸入的音樂訊號及旋紐上的控制訊號綜合而來的。
電腦中,邏輯運算是由 AND、OR、XOR、NOT 及 COPY 幾個基本動作所組成。 除後二者
為線性元件外,均為非線性元件。A. Ekert,D. Deutsch 及 E. Barenco 與 S. Lloyd
分別告訴我們:一個量子電腦, 只要能做 NOT 及任和其它一種非線性運算,就可以達
成全部的運算功能了。[3] 因此,要找到可以製作量子電腦的物理現象並不難。而且,
C. H. Bennett 告訴我們,如果量子電腦是以「可逆邏輯元件」組成的話,那麼計算所
需之最小能量,將與計算之複雜度無關。
其實,全功能的量子元件,早在 50 年代末期,用粒子自旋製造的二位元量子邏輯元件
,就已經存在了。但是,因為他們當時並不是想製造量子邏輯元件,所以他們稱之為雙
共振 (double resonance)。 他們用的是氫原子的電子自旋及其質子自旋;只有當電子
自旋為「壹」時才將質子自旋翻轉;這就是 Controlled- NOT。 他們已可做到 NOT 及
COPY。 後來,E. Barenco,D. DiVincenzo,T. Sleator 及 H. Weinfurter 也證明,
如果能將電子及質子之自旋只翻轉一半就可做到 AND。其它可以作為量子電腦元件的東
西,例如:鹽的晶體;有兩種離子各帶一個自旋。 聚合鍊的電子態、馬荷 - 然德干涉
儀 (Mach-Zehnder interferometer) 也都可以。[4]
這些邏輯元件只要連起來就可做成量子電腦了!但是怎麼連呢?在傳統電腦裡是用金屬
線。它傳遞的其實是電壓訊號。但是要連接這些量子電腦的雙共振閘可就難了;總不能
把原子拆開來,取出自旋,再原封不動的裝回去吧?不過,研究人員也已經想出好方法
了:例如,光纖或空氣中的光子, 都可以作為傳遞自旋資訊的媒介。 加州理工學院的
H. Kimble 有更好的方法:設法在一個小共振腔內,關一個原子及一堆光子;如此,可
以增強微弱的光子與空腔間之交互作用,使得輸入輸出管道間的傳輸更有效。這樣做成
的邏輯元件,當一個光子來讀取資訊時,另一個光子可以翻轉一半。這樣做成的電腦不
但快,而且不容易受外界的干擾而出錯。不過,它還是有一些 Landauer 早就預見的問
題:尤其是,所有元件間的光程,必須精確到幾分之一個所使用的光波波長。
茵斯不魯克 (Innsbruck) 大學的 T. Pellizzari, S. A. Gardiner, J. I. Cirac 及
P. Zoller 等人,最近也想出了, 用阱中原子的日曼基態 (Zeeman ground state) 能
階來做量子運算。如此,可將外界的干擾減低到只有在運算時才會發生。[5,6] 要處理
這個資訊前,必須先將之傳到一個暫存器去。 美國國家標準局的 D. Wineland 就試製
過一個這樣的電腦。[7] 但是,現在能處理的資訊,大概都是幾十到幾百個位元而已。
不過,即使只是一個位元的量子電腦,也能做到一般電腦做不到的事:在「自然」狀態
下去讀取一個量子電腦的狀態,有一半的機率可以讀到「零」,一半的機率可以讀到「
壹」。 這可是最好的隨機變數! 一般電腦裡的隨機變數, 其實都是假的
(pseudo-random number);根據一定的公式算出來的東西,怎可能是「隨機」變數呢?
假如,現在有一個擁有兩個位元的量子電腦,我們想要從一個位元將資訊抄到另一個位
元。如果本來要抄的狀態是 | 0 > 或者 | 1 > 都沒有問題,抄過去都是和原來一模一
樣;當然,抄的時候,我們必須用一個雷射光,先去讀第一個位元的資訊,再去寫第二
個位元的資訊。但是當第一個位元是一個介於 | 0 > 與 | 1 > 間的狀態時問題就來了
:量子力學告訴我們, 任何一個測量,都會把這樣的一個狀態變成 | 0 > 或變成 | 1
>。因此抄過去以後,兩個都變成 | 0 > 或者兩個都變成 | 1 >。這個現象是量子電腦
特有的,叫做不可移植性 (nonclonability)。 當然,有一些資訊就在這個讀取的過程
中遺失了。一個本來就不確定的狀態是不能複製,也不能觀測而不干擾它的。
當有兩個以上的位元時,還會產生所謂的纏結態 (entangled states);例如,| 0 1 >
- | 1 0 > 這種既不屬於 | 0 > 也不屬於 | 0 > 的狀態也是量子電腦所特有的。
量子電腦
前面所說的邏輯元件,每一個都可以用一個么正矩陣 (unitary matrix) 來代表。因此
所謂的「量子計算」就是將系統的聚相態做么正轉換。當位元數目增加後,我們就可用
它來模擬任何量子系統;甚至,包含系統與環境的交互作用。費因曼早已注意到:一般
電腦若要模擬量子系統,所需的時間會隨系統大小成指數增長。然而量子電腦模擬所需
的時間只與系統大小成正比。一個 40 位元的量子電腦在百步之內所能模擬的量子系統
,一般電腦要可能需要 1012 位元花上數年的時間。費因曼告訴我們:用量子電腦來即
時 (real time) 模擬量子系統,在理論上,是可能的; 只要設計個能平行處理的量子
電腦就可以了。但是,若想用古典電腦來即時模擬量子系統,卻是理論上也行不通的!
量子電腦怎能做到這麼快呢?原來它的每一個位元都是同時有「零」,同時也有「壹」
存在而疊加在一起的。因此,從起始值開始,它就是同時代表了所有可能的的狀態。所
有可能的情況都一次算掉了。 這就是 Deutsch 所稱的量子平行處理 (quantum
parallelism)。
量子平行處理聽起來很奇怪嗎?想一想,聲波的例子:如果「零」與「壹」各代表某個
頻率的聲波。那麼,一個聚相態就是一個和聲了。正如和聲,聽起來和各別的單音不同
,這種組成之量子態亦然。但是,無論是和聲或聚相態,兩個波都會互相干涉。量子電
腦就好像交響樂演奏一樣,您聽到的是和聲,而不是單獨的樂器。
Shor 就是利用這種「和聲」的特性來做因數分解。 他告訴我們,因數分解的結果會,
像交響樂團的各個樂器,各有自己的音域而分出來。目前,無論是電腦中、銀行中或者
軍事上,傳遞訊息所用的密碼,都是利用到傳統電腦無法在有限的時間內找出一個做為
「鑰匙」的大質數。有了量子電腦後,這一切就要改觀了。量子電腦可以在短時間內找
到這個「鑰匙」。但是,大家也不必擔心。如果真有那一天,我們也不會再用古典的方
法傳遞資訊。如果用量子方法傳遞密碼,對手要想半途竊聽幾乎是不可能的。事實上,
人們已經在日內瓦湖底,建了一個 23 公里長的此種通訊光纖。[8]
再一個問題是錯誤更正:量子電腦無論是對系統的時間、振幅、相位的要求均很嚴格。
當一個系統的狀態與它的環境狀態纏結在一起時,錯誤就會發生了。量子電腦,必需「
和聲」不受外界的干擾而「走音」 (decoherence)。我們必須在「走音」之前完成計算
。這也是與古典電腦不同的地方:以前,一個計算能否完成,全視使用者所擁有的電腦
記憶體及電腦時間而定。現在,則是要看這個聚相態的壽命了。古典的錯誤更正方法,
都是要測量每個位元後,才知道它們是否有錯。但是量子電腦不可採用這個方法,因為
測量的結果更會使聚相態「走音」。因此我們必需另相它法。對於聚相態最嚴格的要求
是,整個系統不能有一個位元「走音」。不過 Shor 告訴我們,它的因數分解方法在「
走音」不太嚴重時仍然可用。一種更正錯誤的方法是:同時做好幾個相同的計算,不斷
對某些狀態做比較。但是我們並不清楚這種方法的實際效率;而且這也和錯誤的種類有
關。如果這些錯誤並非一起發生,Shor 又告訴我們,只要把資訊複製九份就夠了![9]
事實上,隨著量子電腦而來的革命性改變還很多:在通訊方法上、計算方法上以及測量
方法上,都會有相當的改變。總而言之:在量子電腦成為事實以前,我們還有很長的路
要走。如果量子電腦真的成為事實,量子力學將更加與日常生活息息相關了。
參考資料
1. H. F. Chau and F. Wilczek, Physical Review Letters, 75, 748-750 (1995)
"Simple Realization of the Fredkin Gate Using a Series of Two-Body
Operators".
2. B. Schumacher, Physical Review A, 51, 2738-2747 (1995) "Quantum Coding".
3. S. Lloyd, Physical Review Letter, 75, 346-349 (1995) "Almost Any Quantum
Logic Gate is Universal".
4. S. Lloyd, Science, 261, 1569-1571 (1993) "A Potentially Realizable Quantum
Computer".
5. J. I. Cirac and P. Zoller, Physical Review Letter, 74, 4091-4094 (1995)
"Quantum Computations with Cold Trapped Ions".
6. T. Pellizzari, S. A. Gardiner, J. I. Cirac and P. Zoller, Physical Review
Letter, 75, 3788-3791 (1995) "Decoherence, Continuous Observation, and
Quantum Computing: A Cavity QED Model".
7. C. Monroe, D. M. Meekhof, B. E. King, W. M. Itano and D. J. Wineland,
Physical Review Letters, 75, 4714- 4717 (1995) "Demonstration of a Fundamental
Quantum Logic Gate".
8. A. Muller, H. Zbinden and N. Gisin, Nature, 378, 449-449 (1995)
"Underwater Quantum Coding".
9. P. W. Shor, Physical Review A, 52, 2493-2496 (1995) "Scheme for Reducing
Decoherence in Quantum Computer Memory".
其它參考資料
1. S. Lloyd, Scientific American, October,44-50, (1995) "Quantum-Mechanical
Computers".
2. C. H. Bennett, Physics Today, October, 24-30, (1995) "Quantum Information
and Computation".

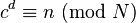

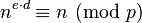 和
和